Observation Definitions
The observations provide the primary (and only) measure that informs the optimization algorithm about the model-to-measurement misfit. For each observation FePEST requires:
-
its type (e.g., hydraulic head, fluid rate budget),
-
its location (e.g. an observation coordinates, stored nodal selection),
-
the time at that it was recorded (in case of a transient model) and
-
the value that was observed in reality.
In many cases the observation definitions are created based on FEFLOW Observation Points. Supported observation types are all observations of system state (e.g., hydraulic head, saturation, mass concentration, temperature and age species) and rate and/or period budget values (fluid, mass and heat) depending on the models FEFLOW Problem Class. Reference values are constant or time-varying values depending on the problem state (steady or transient).
Advanced users may also use IFM plug-ins or the FEFLOW Python Interface to define a customized observation definition. See details in Customization section.
Observation Weights
The definition of the measurement objective function used by GLM and iES algorithms support observation weights.
The weight of an observation controls how strong its residual (the deviation between computed and measured result) contributes to the measurement objective function. A reasonable choice of weights can positively influence the convergence behaviour and result of the optimization.
Different weighting strategies can be applied (alone or in combination), some examples are given in the following.
If using PEST++ GLM or PEST++ IES, users shall be made aware that observations weights have a more important meaning than in classic PEST, and should pay attention to 9.1.6. The weights shall be the inverse of the standard deviation of the measurement uncertainty if using default settings.
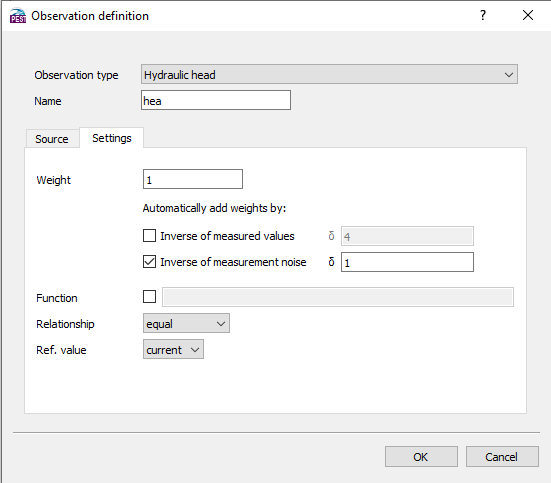
Definition of observation weights.
Weighting by Absolute Measurement Value
The absolute values of observations in a PEST optimization can encompass several orders of magnitudes, especially (but not limited to) if observations of different types are involved (e.g., Hydraulic head [m] and Mass concentrations [mg/l]).
Observations with small values are therefore under-represented in the measurement objective function. Normalizing the values by assigning a weight equal to the inverse of the absolute compensates for this effect and makes sure that the information contained in these values finds appropriate representation in the optimization.
This calculation can be performed by FePEST automatically in the Observation Definition dialog.
Weighting by Measurement Noise
A common strategy of adjusting observation weights is applying the inverse of its expected measurement noise as a weight factor. The contribution of less trustworthy observation values to the measurement objective function is reduced, limiting the risk of inaccurate measurements having a negative impact on the optimization and leading to the estimation of parameter values which are thereby in error.
This calculation can be performed by FePEST automatically in the Observation Definition dialog.
Weighting by a Function
Parameters can be defined as a function of multiple parameters. E.g. instead of calibrating against the absolute value of a measured water level, the difference to the water of a nearby observation location can be used.
Relationship
When using PEST++ (PEST-GLM or PEST-IES), it is possible to restrict the contribution of a measurement to the objective only if its value is above or below it target value. This is useful for example to inform the optimizer that the water level at a specific location must not exceed the topography or the discharge from a spring was measured zero at certain time.
Equalizing Observation-Group Contributions
Observations of different types are assigned to different observation groups. One may also decide to manually assign observations of the same type to different observation groups. Using a spreadsheet or the PEST tool PWTADJ1 observation weights can be adjusted to equalize the total contribution of each observation group to the total objective function at the start of the optimization process. This helps to ensure that the information that is contained in each of these observation groups is used in estimation of model parameters, and not undervalues or overvalued because of too low or too high a contribution to the initial objective function.
De-clustering
Observations can be correlated. Water level measurements at observation wells close to each other are often not independent. It is likely that values and changes at these wells are similar, and the worth of information contributed by one well is diminished because it was already contributed by a different well in its vicinity. The worth of the information provided by each of the wells is therefore lower than a separate measurement at a larger distance. In this case, the weight of correlated observations should be reduced.
Time series are good examples of this principle as well. Daily measurements of the groundwater level might carry the same worth of information as a measurement taken on a monthly basis does. Because the daily measurement has more measurement points, it would be over-represented if the weights of each of these measurement points are not compensated for. This makes it advisable to normalize the weights of observations of time series by the sampling rate of the measurement.
|
|
Further reading: PEST Manual (5th Ed.), Chapter 2.1.2: Observation Weights. |
Observations as a Function of Other Observations
Observations can be defined as a function of other observations. This is useful e.g. to calibrate against the difference between neighboring observation. The respective setting can be defined in the observation definition settings in FePEST or - more often - by editing the observation table in the Problem settings directly e.g. using Excel.
Inequality Constraints
This feature is only available when using the PEST-GLM or PEST-iES operation modes (using PEST++). The options allows to remove an observation from the objective function if the modelled value is above or below the target value. This is useful e.g. where a sensor reading has maxed out or the water level has fallen below the pressure probe. The setting can be set using teh Relationship option in the observation definition settings.